Ajude seus alunos a se preparem para a OBMEP, a Olimpíada Brasileira de Matemática das Escolas Públicas e Particulares.
Esta lista possui questões originais, inspiradas nas questões da OBMEP para o Mirim 2 (4º e 5º anos). Todas as questões possuem respostas explicadas.
Questão 1
Quatro amigas — Ana, Bruna, Camila e Daniele — estão contando suas figurinhas. Ana tem 80 figurinhas, Bruna tem 30 e Camila tem 40. Elas sabem que a quantidade de figurinhas de Ana somada à de Bruna é igual à soma da quantidade de figurinhas de Camila e Daniele. Sabendo disso, qual é a quantidade de figurinhas de Daniele?
O que sabemos?
- Ana tem 80 figurinhas.
- Bruna tem 30 figurinhas.
- Camila tem 40 figurinhas.
A quantidade de figurinhas de Ana mais a quantidade de Bruna é igual à quantidade de figurinhas de Camila mais a quantidade de figurinhas de Daniele.
Então, precisamos descobrir quantas figurinhas Daniele tem.
Passo 1: Somar as figurinhas de Ana e Bruna.
Ana tem 80 figurinhas e Bruna tem 30. Vamos somar:
80 + 30 = 110 figurinhas
Passo 2: Encontrar a quantidade de figurinhas de Daniele.
Sabemos que a quantidade de Ana + Bruna (110) é igual à quantidade de Camila + Daniele. Como Camila tem 40 figurinhas, agora descobriremos quantas figurinhas Daniele tem.
A quantidade de figurinhas de Daniele é o que falta para completar 110. Quanto falta é uma ideia de subtração.
110 – 40 = 70
Então, Daniele tem 70 figurinhas.
Questão 2
No restaurante Comida Legal, há dois tipos de assentos.:
Sabendo que, ao todo, há 21 pés entre os assentos, quantos bancos com três pés e quantos bancos com quatro pés há no restaurante?
A) 2 bancos com três pés e 3 bancos com quatro pés.
B) 3 bancos com três pés e 3 bancos com quatro pés.
C) 4 bancos com três pés e 3 bancos com quatro pés.
D) 5 bancos com três pés e 2 bancos com quatro pés.
E) 6 bancos com três pés e 1 bancos com quatro pés.
Vamos resolver o problema passo a passo:
Total de pés é 21.
Testaremos as opções fornecidas:
A) 2 bancos com três pés e 3 bancos com quatro pés:
3×2 + 4×3 = 6 + 12=18 (não é 21)
B) 3 bancos com três pés e 3 bancos com quatro pés:
3×3 + 4×3 = 9+12 = 21 (essa opção está correta!)
C) 4 bancos com três pés e 3 bancos com quatro pés:
3×4 + 4×3 = 12+12 = 24 (não está correta)
D) 5 bancos com três pés e 2 bancos com quatro pés:
3×5 + 4×2 = 15+8 = 23 (não é 21)
E) 6 bancos com três pés e 1 banco com quatro pés:
3×6 + 4×1 = 18+4 = 22 (não é 21)
Portanto, a resposta correta é B) 3 bancos com três pés e 3 bancos com quatro pés.
Questão 3
Ana, Beatriz, Carlos, Daniel e Eduardo são amigos e participaram de uma gincana em que precisaram formar dois grupos. Sabemos que:
- Eduardo não está no mesmo grupo que Beatriz e Daniel;
- Ana não está no mesmo grupo que Carlos e Daniel;
- Um grupo terá três crianças.
Com base nessas informações, quem está no mesmo grupo que Ana?
O que sabemos?
- Existem 5 amigos: Ana, Beatriz, Carlos, Daniel e Eduardo.
- Eles foram divididos em dois grupos.
- Um grupo possui três crianças e o outro apenas duas.
- Eduardo não está no mesmo grupo que Beatriz e Daniel.
- Ana não está no mesmo grupo que Carlos e Daniel.
Nosso objetivo é descobrir quem está no mesmo grupo que Ana.
Passo 1: ver quem não pode estar no grupo de Ana.
Sabemos que Ana não está no mesmo grupo que Carlos e Daniel. Então, Carlos e Daniel estão no outro grupo.
Agora, já sabemos que Carlos e Daniel não estão no grupo de Ana.
Passo 2: verificar quem sobrou.
Os amigos que ainda podem estar no grupo de Ana são: Beatriz e Eduardo.
Passo 3: verificar as informações sobre Eduardo.
Sabemos que Eduardo não está no mesmo grupo que Beatriz e Daniel. Como Daniel já está no outro grupo, isso significa que Eduardo também não pode estar no grupo de Beatriz.
Então, Eduardo tem que estar no mesmo grupo que Ana.
Passo 4: ver quem está no grupo de Beatriz.
Se Eduardo não pode estar com Beatriz, então Beatriz está no grupo com Carlos e Daniel.
Conclusão: Eduardo é a única pessoa que está no mesmo grupo que Ana.
Questão 4
Uma colmeia é formada por alvéolos na forma de hexágonos, figuras que possuem seis lados. Quando novos alvéolos são adicionados, alguns dos lados se sobrepõem. Se começarmos com dois alvéolos conectados, o número de lados da colmeia será 11.
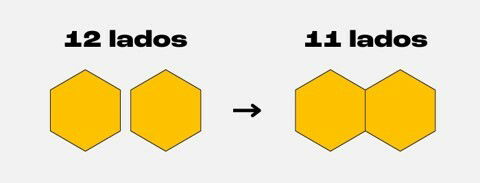
Qual o número mínimo de lados dessa colmeia após acrescentar 2 alvéolos?
Cada alvéolo (hexágono) tem 6 lados, mas quando eles se juntam, alguns lados são compartilhados.
Quando começamos com dois alvéolos, eles compartilham um lado, por isso a colmeia tem 11 lados. Agora, quando adicionamos mais dois alvéolos, eles também compartilham lados com os alvéolos já presentes.
Para ter o menor número de lados, devemos juntar os hexágonos sobrepondo o maior número de lados possíveis.
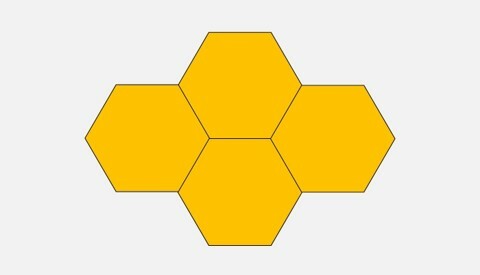
Após adicionar dois novos alvéolos, o número mínimo de lados da colmeia será 19.
Questão 5
As sandálias na figura são todos do mesmo modelo, cor e tamanho. Os pés (direito e esquerdo) estão embaralhados.
Quantas sandálias estão sem par?
Um par é formado por duas sandálias, uma esquerda e uma direito. Juntando os pés, vemos que uma sandália apenas está sem par.
Questão 6
Considere as malhas quadriculadas apresentadas na imagem abaixo.
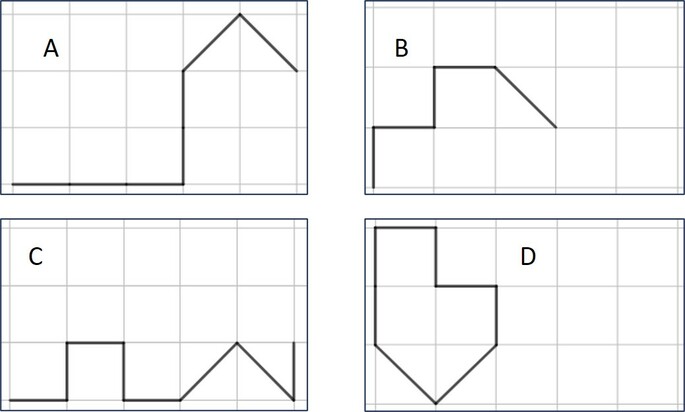
Podemos afirmar que:
A) Trajetória A é a mais curta.
B) Trajetória B é a maior.
C) Trajetória C é a maior.
D) Trajetórias C e D possuem mesmo comprimento.
E) Todas têm o mesmo comprimento.
- A trajetória A possui 5 traços pelos lados dos quadrados e duas diagonais.
- A trajetória B possui 4 traços pelos lados dos quadrados e uma diagonal.
- A trajetória C possui 6 traços pelos lados dos quadrados e duas diagonais.
- A trajetória D possui 6 traços pelos lados dos quadrados e duas diagonais.
Assim, as trajetórias C e D possuem mesmo comprimento.
Questões para OBMEP (Olimpíada de Matemática):
Você também pode se interessar por:
Referências Bibliográficas
OLIMPÍADA MIRIM OBMEP. Olimpíada Mirim OBMEP. Disponível em: https://olimpiadamirim.obmep.org.br/. Acesso em: 24 out. 2024.
ASTH, Rafael. Questões para Olimpíada Mirim 2 OBMEP (com soluções explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/questoes-para-olimpiadas-mirim-2-obmep/. Acesso em:
